只是单纯的讨论这起交通事故车内成员所承受的加速度是多少

一般人能承受4~8个G加速度过载，极少数人可以承受10G的加速度。

本文用物理力学知识分析这次交通事故中车内乘员所承受的加速度范围。

假设他们碰撞在一起后一起运动，根据动能守恒公式计算碰撞后的速度：

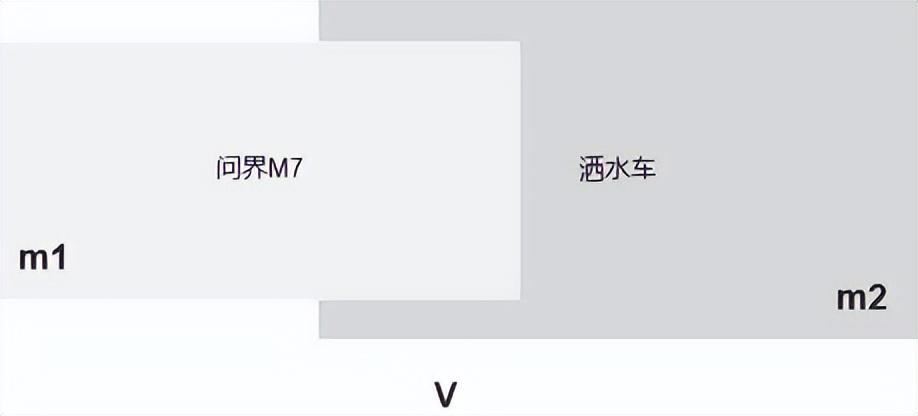
m1v1+m2v2=(m1+m2)v

其中质量单位是kg、速度单位是m/s

这里假设碰撞后两车速度一样，未计算车辆吸能部分。

根据官方通报M7碰撞时速度为：

v1=115km/h=115*1000/3600=31.94444...m/s

M7整备质量2370kg，两大人按120kg算，小孩按25kg算。

小车参与碰撞时的质量:

m1=2370+120+25=2515kg

洒水车总质量未知，一般城市用洒水车载水量是2吨到15吨之间，假设该事故中洒水车质量为：

m2=10000kg

关于洒水车速度，有一段采访表明洒水车是行驶作业，具体车速是多少未知，这里假设按30km/h计算。

v2=30*1000/3600=8.3333...m/s

代入公式：

m1v1+m2v2=(m1+m2)v

2515*31.94+10000*8.33=(2515+10000)v

解得：v=13.0746m/s=47.068km/h

车长5020mm轴距2820mm，假设吸能长度为车长减轴距的一半，也就是大概前发动机舱的长度。计算出吸能位移s=(5020-2820)/2=1100=1.1m

看问界官方给的事故模拟图，碰撞已经入侵到前排司机位置，如果没有入侵到后排，对后排乘员来说，吸能位移大约为车长的一半也就是2.51m比较准确。

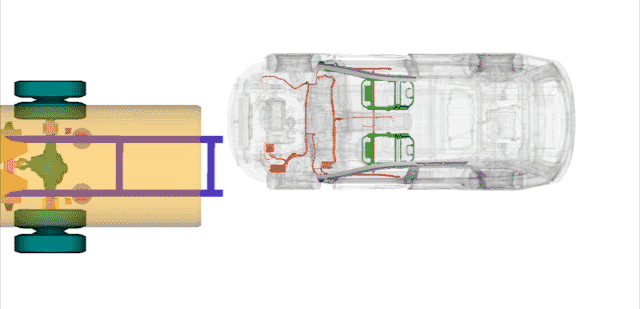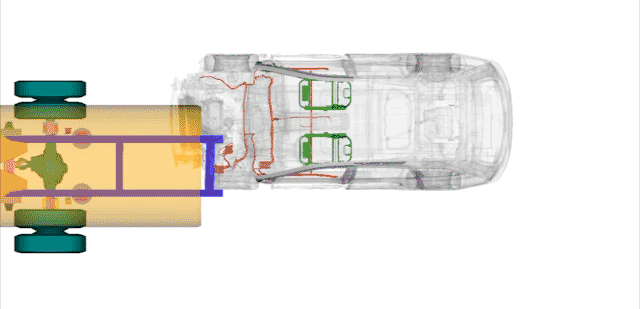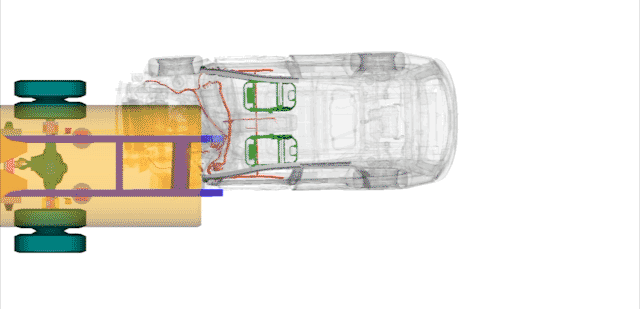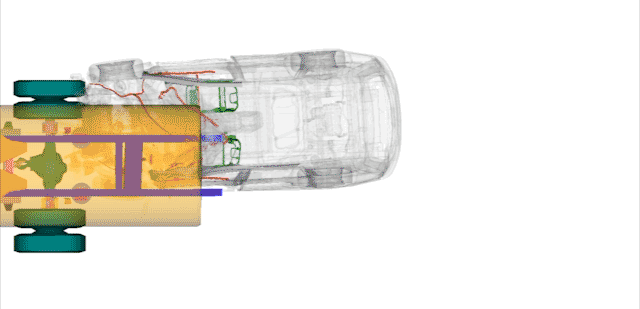
发生碰撞时洒水车速度从30km/h飙升到47.068km/h；

M7从115km/h减速至47.068km/h，他们所用的时间是一样的。

假设碰撞吸能是均速直线运动，也就是加速度a是恒定的。

两车碰撞速度相等时问界M7发生位移为s1，洒水车发生位移为s2，

并且s1-s2=吸能长度s，也就是2.51米。

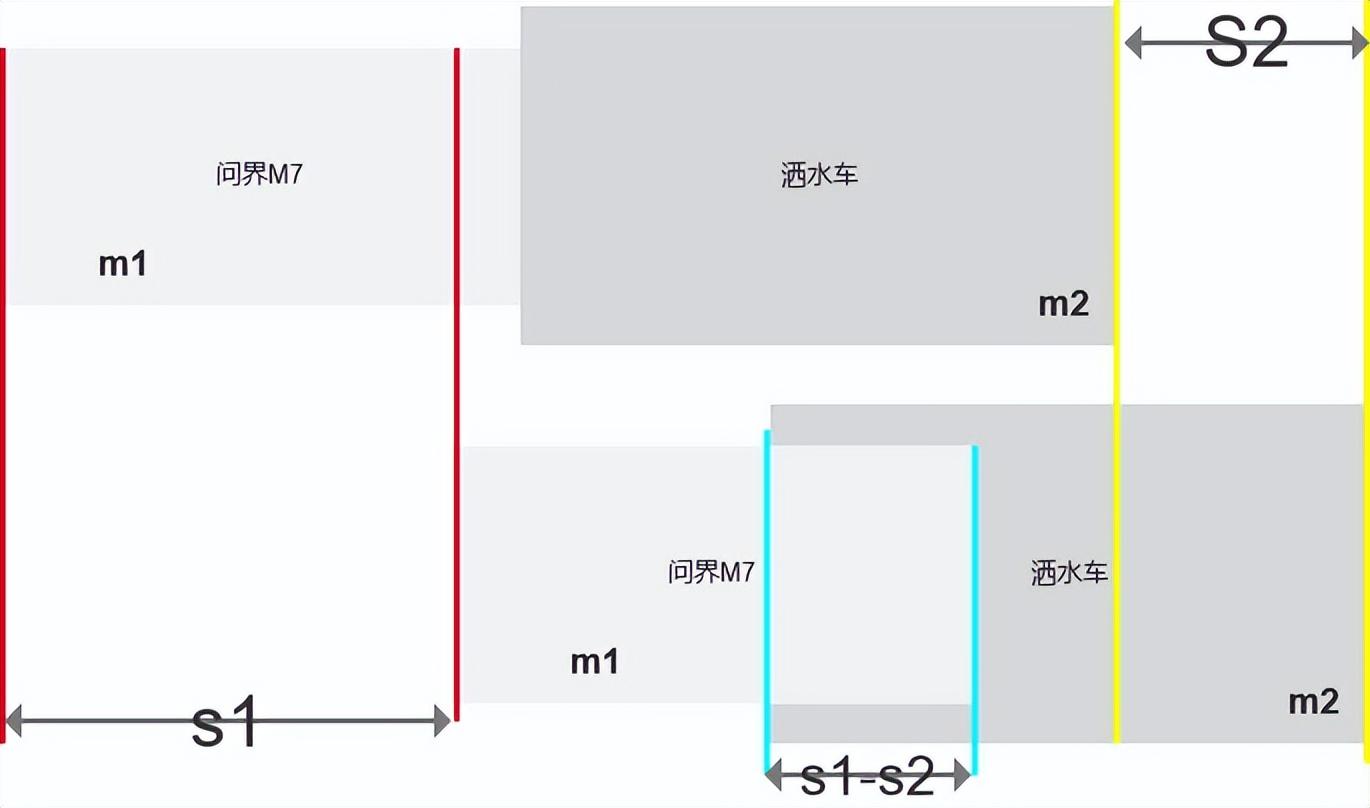
根据均加速直线运动位移公式

s1=v1t-1/2*a1t²

s2=v2t+1/2*a2t²

s1-s2=2.51

这里v1是问界M7碰撞前的速度115km/h也就是31.94444...m/s，v2为洒水车初速度，a1是碰撞后问界M7减速的加速度，a2是碰撞后洒水车加速的加速度，t是从115km/h变成碰撞后所需要的时间。

再根据匀加速直线运动的速度公式

a1=(v-v1)/t

a2=(v-v2)/t

代入上面方程：

s1=(v+v1)t/2=22.50952t

s2=(v+v2)t/2=10.70395t

所以：

t=0.212611s

求得问界M7加速度a1

a1=(13.0746-31.94444)/0.212611=-88.75288m/s²

g=9.8m/s²

a1/g=9.056

也就是说后排成员过载9.0564个G，注意，这个还没算吸能导致能量损失，所以后排成员过载比9.0564个G要小。

根据一般人只能承认承受4~8个G只差一个G，也就是说只要吸能大于1个G后排成员就有很大概率存活。

再计算一下洒水车

a2=(13.0746-8.3333)/0.212611=22.30035m/s²

a2/g=2.2755

洒水车上成员过载只有2.2个G，在系安全带的情况大概率毫发无损。

最后为了安全，安全带记得一定要系，不管是前排还是后排，它是保命的最后一道防护。剩下的你只能交给车的被动安全了，只能听天由命，祈祷你的车被动安全能保护你了。

以上数据基于理想模型计算，不能代替现实碰撞。仅供参考。有错误欢迎指正！